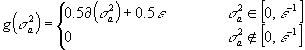Factores de Bayes para la heredabilidad de los caracteres cuantitativos
L.A. García-Cortés,1 C. Cabrillo, 2 C. Moreno1 y L.Varona3
1
Unidad de Genética Cuantitativa. Universidad de Zaragoza. C/ Miguel Servet, 177. 50013-Zaragoza. 2Departamento de Física. CSIC. Madrid. 3Área de Producción Animal, Centro UdL-IRTA, 25198-Lleida.
Gelman y colaboradores (1995) opinan que generalmente los contrastes puntuales sobre variables continuas no son razonables. Por ejemplo, sugerir que la probabilidad de que un componente de varianza sea exactamente cero no tiene sentido salvo en raras ocasiones.
En este trabajo consideraremos que el análisis de los caracteres cuantitativos de los animales es uno de los campos donde este contrastes esta justificado. La heredabilidad de un carácter implica la presencia de genes que no están fijados en la población a estudiar. Los caracteres no regulados por estos genes presentarían una heredabilidad nula, y por tanto, la probabilidad de que un componente aditivo de la varianza sea exactamente cero no es en ningún caso despreciable a priori.
Sin embargo, cuando se desea realizar un contraste de hipótesis cerca del extremo del espacio paramétrico de una variable, las propiedades asintóticas de los test de razón de verosimilitudes fallan (Stram y Lee, 1994). Los métodos bayesianos no son sencillos de usar para los contrastes sobre componentes de varianza debido en general al uso de a prioris impropias sobre este tipo de variables.
Berger y Sellke (1987) propusieron un método bayesiano para realizar el contraste de hipótesis nulas que se basa en la incorporación de una probabilidad discreta en la distribución a priori de la variable objeto del contraste. Este método ha sido empleado con éxito para realizar contrastes de comparación de medias (Berger y Deely, 1988), pero no ha dado buenos resultados en los contrastes de componentes de varianza.
En este trabajo mostramos que el método de Berger y Sellke anteriormente citado no produce buenos resultados cuando se pretende contrastar la hipótesis nula sobre componentes de varianza, pero que al realizar una reparametrización del modelo similar a la desarrollada por Theowald y col (1997), el análisis bayesiano permite asignar una probabilidad posterior a la hipótesis nula y calcular el factor de Bayes con una relativa facilidad.
La esencia del método descrito por Berger y Sellke (1987) consiste en asignar un "punto de masa" en el valor cero de la distribución a priori de la variable a contrastar.
Supongamos que queremos contrastar 
para la hipótesis nula 
, y su
distribución a priori convencional es 
. Suponemos también
que la probabilidad a priori de que la hipótesis nula sea cierta es del 0,5. El
procedimiento presentado aquí consiste en redefinir la distribución a priori de 
como 
.
Donde 
es la distribución delta de Dirac, la versión
continua de la distribución degenerada discreta en el punto cero.
Tras el análisis bayesiano, la probabilidad posterior de ambas hipótesis puede calcularse así
(1)
(2)
Y el factor de Bayes en contra de la hipótesis nula es
Así el contraste de la hipótesis nula solo requiere la ordenada en cero de la distribución marginal posterior de un análisis bayesiano convencional.
CONTRASTE SOBRE EL COMPONENTE DE VARIANZA ADITIVO
En esta sección trataremos realizar el contraste
sobre el componente de varianza aditivo usando las fórmulas (1) y (2). En este caso es
sencillo mostrar que el análisis falla. Omitimos el limite 
en las expresiones para ganar en claridad.
La distribución a priori propia para el componente de varianza aditiva es
En este caso, si tenemos en cuenta que 
puede hacerse tan pequeño como se quiera, las fórmulas (1) y
(2) dan un resultado incoherente
Es decir, sea cual sea el resultado del análisis convencional, la evidencia a favor de la hipótesis nula es total. Este resultado no ha de entenderse como que le método no funciona para este modelo, sino que este método pone de manifiesto que el modelo es incorrecto.
Casella y Berger (1987) muestran que a prioris que concentran masas de probabilidad en un punto pueden conducir a probabilidades posteriores extremas, dependiendo de la estructura de la distribución a priori.
CONTRASTE SOBRE LA HEREDABILIDAD
En esta sección reparametrizamos el modelo de forma que las observaciones se expliquen a partir de la varianza total y el coeficiente de heredabilidad. Este modelo es similar al descrito en Theowald y col (1997), aunque ellos usan la varianza residual en lugar de la varianza total.
En este modelo alternativo, que desarrollaremos
sobre un modelo macho, 
y 
.
La distribución a priori para 
se expresa como
,
Teniendo en cuenta que 
, las probabilidades posteriores para las hipótesis nula y
alternativa son respectivamente
RESULTADOS
Se analizaron 9 casos con 20 réplicas simuladas. En todos los casos, el número de datos fue 10 veces mayor que el número de machos. El análisis bayesiano se realizó con un algoritmo de Gibbs y las densidades marginales en el punto cero fueron calculadas usando el argumento de Rao-Blackwell. La longitud de la cadena fue de 1100 y se descartaron los 100 primeros ciclos. Las cadenas necesarias en este caso son pequeñas al haber integrado analíticamente los efectos aleatorios del modelo, los tamaños efectivos de las cadenas en los 180 análisis realizados oscilaron entre 287 y 779 usando el método de Geyer (1992).
La tabla 1 presenta la media de las ordenadas en cero del análisis convencional, la media de las probabilidades posteriores de la hipótesis nula, y la clasificación de los factores de Bayes según Kass y Raftery (1995).
Caso |
|
Machos |
|
|
BF(1/0)* |
BF(0/1)* |
| 1 | 0 | 50 | 8.2753 | 0.8401 | 20-0-0-0 | 4-10-6-0 |
| 2 | 0.1 | 50 | 4.4263 | 0.7030 | 20-0-0-0 | 10-8-2-0 |
| 3 | 0.2 | 50 | 2.1099 | 0.4394 | 13-3-3-1 | 16-3-1-0 |
| 4 | 0 | 100 | 11.4483 | 0.8931 | 20-0-0-0 | 2-6-12-0 |
| 5 | 0.1 | 100 | 1.8600 | 0.4544 | 14-1-4-1 | 17-3-0-0 |
| 6 | 0.2 | 100 | 0.2785 | 0.1561 | 3-10-2-5 | 20-0-0-0 |
| 7 | 0 | 200 | 20.8802 | 0.9430 | 20-0-0-0 | 0-0-0-20 |
| 8 | 0.1 | 200 | 4.0054 | 0.4294 | 12-6-1-1 | 15-3-2-0 |
| 9 | 0.2 | 200 | 0.2203 | 0.0996 | 2-4-5-9 | 20-0-0-0 |
Berger y Sellke 1987. J Amer Stat Assoc. 82:112-122
Berger y Deely 1988. J Amer Stat Assoc. 83:364-373
Casella y Berger. 1987. J Amer Stat Assoc. 82:106-111
Gelman, Carlin, Stern y Rubin. 1995. Chapman and Hall, London.
Geyer. 1992. Stat. Sci. 7:467-511
Kass y Raftery 1995. J. Am. Stat. Assoc. 90:773-795
Stram y Lee. 1994. Biometrics. 50:1171-1177
Theowald, Firat y Thompson. 1997. Genet Sel Evol 29:57-72