CLASIFICACION RACIAL MEDIANTE MICROSATÉLITES

Carleos, C., Baro*, J.A., Carretero†, Y., Checa†, M.L., Dunner†, S., Cañón†, J.

Dpto. de Investigación de ASEAVA. Asturias* Unidad de Mejora Genética, CIATA. Asturias. †Dpto. de Producción Animal. UCM. Madrid

 

INTRODUCCIÓN

La utilización de marcadores genéticos con un elevado grado de polimorfismo, como los microsatélites, en estudios de diversidad genética y de estructura genética de poblaciones se ha generalizado tanto en especies de animales domésticos como silvestres. Asociado a estas aplicaciones ha surgido un interés creciente sobre la posibilidad de utilizar estos mismos conjuntos de marcadores para asignar o rechazar animales o grupos de animales a determinadas poblaciones (Shriver et al., 1997; Götz y Thaller, 1998; MacHugh et al., 1998). Shriver et al. (1997) utilizan un estimador denominado de afiliación étnica (EAE=Ethnic-affiliation estimation) que mide la diferencia entre dos distribuciones,valiendo 0 cuando son iguales y tiende a infinito a medida que divergen. El valor de EAE se obtiene mediante la suma para todos los loci del producto de las probabilidades a priori del genotipo marcador por el logaritmo del cociente de verosimilitudes. Götz y Thaller (1998) proponen un método que permite probar la hipótesis de que un individuo pertenezca a una población frente a la hipótesis de que pertenece a cualquier otra alternativa.

Las aplicaciones pueden ser diferentes y, dependiendo del interés concreto, diferentes serán las hipótesis a contrastar. Así, por ejemplo, puede que el interés consista en probar que un determinado animal con un perfil genético pertenece a una determinada población cuyas frecuencias alélicas son conocidas, resultando difícil definir una población alternativa. Puede, en otro caso, existir el interés de probar la hipótesis de que una muestra pertenece a una población determinada o a otra población alternativa cuyas frecuencias alélicas deben ser conocidas.

Con el fin de probar las posibilidades de estos marcadores polimórficos en alguno de los problemas planteados de asignación o rechazo de animales a poblaciones hemos utilizado dos especies diferentes: bovino y equino, para los que se dispuso de 16 y 13 microsatélites respectivamente.

 

MATERIAL Y METODOS

En la especie bovina utilizamos los resultados de 250 animales pertenecientes a 5 razas (Tudanca, Asturiana de los Valles y de la Montaña, Sayaguesa y Alistana-Sanabresa) y 16 marcadores con un total de 140 alelos. Estos resultados se obtuvieron en el contexto de un proyecto europeo en el que se incluyen 18 razas autóctonas de carne de Francia, España y Portugal (FAIR-CT95-0702). Los datos de la especie equina se obtuvieron de un proyecto financiado por la CICYT (AGF95-0643) y por Caja Asturias y pertenecen a 5 razas de caballos celtas peninsulares y 2 de las Islas Baleares. Se analizaron un total de 532 animales con 13 marcadores que dieron lugar a 120 alelos.

La asignación de un individuo I a una raza de un conjunto R1, ..., Rn se basa en la clásica regla discriminante de máxima verosimilitud, es decir, se asigna a aquella raza que hace máxima la probabilidad de ese individuo condicionado a la raza, lo que equivale a asignar a la raza más probable condicionado al genotipo del individuo bajo la hipótesis de que todas las razas son igualmente probables:

Sea = estimación de la frecuencia del alelo a del locus l en la raza r

Entonces P[ individuo I | raza r ] = donde l recorre los loci marcadores y h(i,l) = 1 si a_il1= a_il2 y h(i,l) =2 si son distintos.

 

El individuo se clasifica en la raza R tal que P[ I | R] es máximo. Para ello se requiere una estimación de las frecuencias alélicas en las diferentes razas. Caso especial es el de que un alelo aparezca con frecuencia cero en una determinada raza. En este caso se puede hacer la consideración de que:

el alelo es absolutamente discriminante para no clasificar en tal raza a cualquier animal portador;

no se dispone de una estimación precisa de la frecuencia de tal alelo, y para evitar la exclusión radical de cualquier portador, se asigna a tal alelo una probabilidad pequeña (pero estrictamente positiva) de aparición en la raza (Shriver et al. proponen 1/(2n+1), siendo n el tamaño de la muestra utilizada en la estimación para tal raza).

Una forma habitual de expresar la significación de un resultado es mediante el LOD= logaritmo decimal del cociente de verosimilitudes. Una consecuencia del procedimiento (b) es que también se evitan las divisiones por cero en los cocientes de verosimilitudes.

Si se prefiere plantear la clasificación de un animal en dos razas mediante un contraste de hipótesis clásico, con hipótesis nula H0: I pertenece a R1, e hipótesis alternativa H1: I pertenece a R2, es preciso obtener la distribución de un estadístico apropiado bajo H0, bien mediante muestreo autosuficiente (bootstrap) o por simulación directa a partir de las frecuencias alélicas. Consideremos el estadístico LOD para denotar el log (P[I|R2] / P[I|R1]). En el caso del bootstrap, se considerarían tantos valores de LOD como individuos tuviera la muestra. Si el tamaño de la muestra es reducido, tendríamos pocos valores como para considerar la distribución del LOD determinada con suficiente precisión. En tal caso, parece más conveniente suponer equilibrio de Hardy-Weinberg y equilibrio de ligamiento (independencia en la segregación de los loci) y generar por simulación individuos a partir de las frecuencias alélicas, es decir, para cada individuo generado, para cada locus, extraer dos alelos según las frecuencias alélicas de la raza en cuestión. De este modo, se puede generar un número arbitrario de individuos de la raza 1 y obtener el LOD para cada uno de ellos, con lo que se obtiene una aproximación por Monte Carlo a la distribución del LOD bajo H0. Como lo lógico es suponer que el LOD será grande para un individuo de la raza 2 (rechazar H0 cuando LOD es grande), se debe buscar el cuantil correspondiente a la cola superior de tal distribución que cubra una probabilidad determinada (probabilidad de error tipo 1). Posteriormente se generan de igual forma un número arbitrario de individuos de la raza 2, se obtienen sus LODs y se aproxima la distribución del LOD bajo H1. La potencia de detección, dado un cierto nivel de error tipo 1, será la proporción de LODs simulado bajo H1 que excedan el umbral calculado en la simulación de los LODs bajo H0.

 

RESULTADOS Y DISCUSIÓN

Los resultados se presentan desde tres perspectivas.

 Con las poblaciones de bovino se generaron genotipos, suponiendo equilibrio HW y de ligamiento, y se calculó la probabilidad de pertenecer a cada una de las razas, lo que permite presentar soluciones a diferentes problemas, por ejemplo: a) se generaron 10.000 individuos de cada una de las 5 razas y se clasificaron siguiendo el criterio de asignar en función de la máxima probabilidad. La probabilidad media de equivocación resultó ser del 1,2 % y por raza fueron, 1 % para la Tudanca, 2,4 % para la Asturiana de los Valles, 1,4 % para la Asturiana de la Montaña, 0,3 % para la Sayaguesa y un 1 % en el caso de la Alistana; b) se puede considerar la situación concreta en el caso de dos razas, simulamos 10.000 animales de la raza Asturiana de los Valles y 10.000 de la de Montañas y contamos el número de veces que esos animales se asignarían a, por ejemplo, la raza Asturiana de la Montaña. Los resultados obtenidos nos dieron que 0,91 % de animales pertenecientes a la raza Asturiana de los Valles se asignan a la otra raza (Asturiana de la Montaña) y un 0,44 % de animales de Montaña se asignan a la de Valles. Se pueden calcular los umbrales correspondientes a un determinado porcentaje de confianza para los dos errores posibles, clasificar Valles como Montaña y Montaña como Valles. Podemos definir, de este modo, una región intermedia de tal manera que un animal que cayera en esa región no sería asignado a ninguna de las razas.

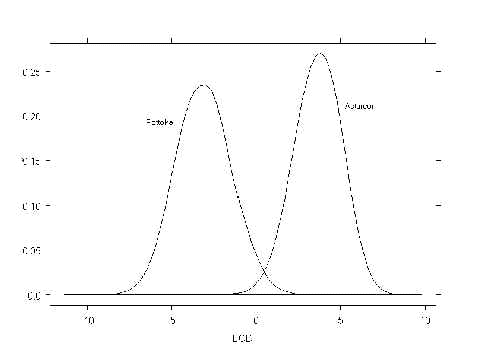
Por último presentamos en la figura las distribuciones de los LODs bajo las hipótesis nula (H0: el animal problema pertenece a la raza Pottoka) y alternativa (H1: el animal problema pertenece a la raza Asturcón) que se corresponde con los siguientes valores de error tipo I y II.

Error tipo I                                0,05     0,01    0,001
Umbral LOD                           -0,42     0,64    1,86
Potencia (1- error tipo II)        99,8     98,5    90,4

 

REFERENCIAS BIBLIOGRAFICAS

Götz, K.-U, Thaller, G., 1998. Assignment of individuals to populations using microsatellites. Journal of Animal Breeding and Genetics, 115:53-62.

MacHugh, D.E., Loftus, R.T., Cunningham, P., Bradley, D.G., 1998. Genetic structure of seven European cattle breeds assessed using 20 microsatellite markers. Animal Genetics, 29: 333-340.

Shriver, M.D., Smith, M.W., Jin, L., Marcini, A., Akey, J.M., Deka, R., Ferrell, R.E., 1997. Ethnic-Affiliation Estimation by use of population-specific DNA markers. American Journal of Human Genetics, 60:957-964.