PROBABILIDAD POSTERIOR DE LA PRESENCIA DE UN QTL.
Luis Varona1, Luis Alberto García-Cortés2
y Miguel Pérez-Enciso1.
1
Centre UDL-IRTA. Area de
Producción Animal. 25198. Lleida.2 Unidad de Genética Cuantitativa y Mejora
Animal. Facultad de Veterinaria. 50013. Zaragoza.
INTRODUCCION.
La detección de loci de expresión cuantitativa
(QTLs) ha cobrado un importante desarrollo en los últimos años. La mayoría de los
procedimientos propuestos en la literatura presentan problemas en cuanto a la definición
del umbral de significación. Por lo tanto, se recurre a test de permutación para
determinarlos (Churchill y Doerge, 1994).
Desde un punto de vista bayesiano, el Factor de
Bayes define en términos de probabilidad la evidencia de diferentes modelos propuestos
(Kass y Raftery, 1995). El cálculo del Factor de Bayes por procedimientos numéricos
presenta problemas de estabilidad (Newton y Raftery, 1995). Por este motivo, se han
utilizado aproximaciones al Factor de Bayes mediante algoritmos de Montecarlo que permiten
calcular la probabilidad posterior de cada modelo (Green, 1995; Hoeschele et al., 1997).
Pese a todo, en comparaciones de modelos jerárquicos, la reparametrización del modelo de
componentes de varianza en términos de correlación intra-clase (García-Cortés et al.,
1999) permite calcular el Factor de Bayes a partir de cualquier metodología que
proporciones muestras de la distribución posterior conjunta, como el muestreo de Gibbs.
El objetivo de este trabajo es presentar un ejemplo del calculo de Factores de Bayes para
la detección de QTLs en una población abierta, así como discutir sus posibles
aplicaciones.
MATERIAL Y METODOS.
Se simuló una población formada por 15 machos que
se cruzaron con 5 hembras cada uno, en cada cruce se produjeron 5 descendientes. El modelo
de simulación fue:
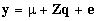
Donde y son los registros fenotípicos, Z
es la matriz de incidencia, q son los efectos aleatorios asociados con el QTL,
distribuidos con mediante una distribución normal multivariante con una matriz de
relaciones (Q) y e son los residuos. Se simulo un QTL infitamente alélico
en posición 30cM, y 4 marcadores completamente informativos en posiciones 0 cM, 20cM,
40cM y 60cM.
Después de integrar el efecto aleatorio (q)
el modelo se reduce a:
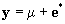
donde:
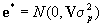
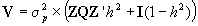
donde h2 es el porcentaje de variación
explicado por el QTL.
El modelo a comparar es:
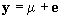
donde:
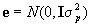
Se usaron distribuciones a-prioris planas para todos
los parámetros en ambos modelos.
El Factor de Bayes entre ambos modelos puede
definirse como:
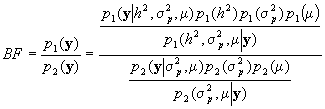
Si se tiene en cuenta que 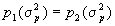 ,
, 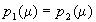 y
y 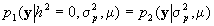
Entonces:
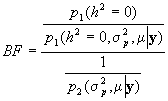
Por lo tanto:
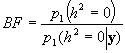
dado que:
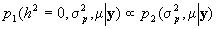
y
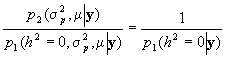
Por lo tanto, para calcular el Factor de Bayes solo
se necesita calcular 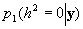 . Esta densidad se
obtiene mediante el argumento de Rao-Blackwell a partir de la observaciones generadas
mediante un muestreo de Gibbs. En este caso, se ha calculado el Factor de Bayes para cada
posición del cromosoma (cada cM).
. Esta densidad se
obtiene mediante el argumento de Rao-Blackwell a partir de la observaciones generadas
mediante un muestreo de Gibbs. En este caso, se ha calculado el Factor de Bayes para cada
posición del cromosoma (cada cM).
RESULTADOS.
Los resultados del Factor de Bayes para cada
posición dentro del cromosoma analizado se presentan en la grafica I. La probabilidad
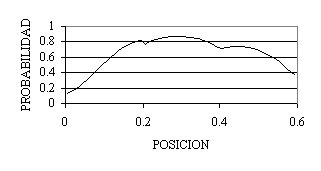
posterior de la presencia de un QTL en dichas posiciones se presenta en la grafica II. La
información presentada es equivalente, el valor que maximiza el Factor de Bayes es 29cM
que presenta un Factor de Bayes de 6.81 y una probablidad posterior de presencia de un QTL
de 0.87.
Gráfica I. Factor de Bayes.
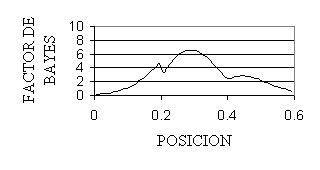
Gráfica 2. Probabilidad Posterior.
DISCUSION.
En este trabajo se presenta un ejemplo de la
utilización de Factores de Bayes para detectar la presencia de QTL. El Factor de Bayes
presenta diferencias con respecto a los procedimientos clásicos de contraste de modelos,
en lugar de detectar evidencia en contra de la hipótesis nula, proporciona la
probabilidad posterior de cada uno de los modelos.
Por otra parte, proporciona algunas ventajas con
respecto a otros procedimientos. En primer lugar, ofrece resultados en términos de
probabilidad, con lo que se evita recurrir a la definición, teórica o numérica, de
umbrales de significación. Además, y como consecuencia, presenta una gran ventaja cuando
se combina información procedente diversos experimentos, con otros procedimientos no es
obvio como combinar distintas fuentes de información, pero en este caso, basta
multiplicar estos valores para obtener el Factor de Bayes conjunto.
Pese a todo, todavía hay diferentes aspectos en los
que seguir trabajando, por una parte, el Factor de Bayes presenta dependencia con respecto
a las distribuciones a-priori asumidas, por lo que debe ser especialmente cuidadoso al
determinarlas, siendo conveniente realizar análisis de sensibilidad.
Por otra parte, hay que ser conscientes que los
modelos contrastados, en este caso son, 1) Modelo sin QTL y 2) Modelo con un QTL en una
determinada posición. Para solucionar este problema existen varias alternativas que
permitirán en el futuro refinar los análisis. 1) Consideración de efectos poligénicos,
2) Integrar la posición dentro del análisis y 3) consideración de distintos segmentos a
lo largo del genoma como efectos.
REFERENCIAS
- Churchill y Doerge, 1994. Genetics 138:963-971.
- García-Cortés et al., 1999. En preparación.
- Hoeschele et al., 1997. Genetics 147:1445-1457.
- Green, 1995. Biometrika 82:711-732.
- Kass y Raftery, 1995. Journal of the American
Statistical Association. 90:773-795.
- Newton y Raftery, 1994. J. Roy. Statist. Soc. B.
56:3-48.
.
Agradecimientos : Trabajo financiado gracias
al proyecto BIO-CT97-962243 (UE).
![]()
![]()
![]()
![]()
![]()
![]()
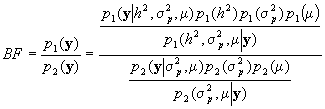
![]() ,
, ![]() y
y ![]()
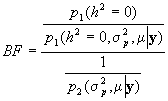
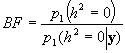
![]()
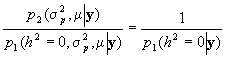
![]() . Esta densidad se
obtiene mediante el argumento de Rao-Blackwell a partir de la observaciones generadas
mediante un muestreo de Gibbs. En este caso, se ha calculado el Factor de Bayes para cada
posición del cromosoma (cada cM).
. Esta densidad se
obtiene mediante el argumento de Rao-Blackwell a partir de la observaciones generadas
mediante un muestreo de Gibbs. En este caso, se ha calculado el Factor de Bayes para cada
posición del cromosoma (cada cM).
