EL MAPEO DE SEGMENTOS,

UNA ALTERNATIVA AL BARRIDO GENOMICO PARA LA IDENTIFICACION DE QTLS

Miguel Pérez-Enciso y Luis Varona

Centro UdL-IRTA, Area de Producción Animal, 25198 Lleida

 

ANTECEDENTES

La técnica habitual para la identificación de loci que afectan a caracteres de expresión cuantitativa (QTLs) es el barrido genómico (‘genomic scan’). El proceso se puede dividir en tres etapas: 1) Definición de un modelo puntual, normalmente uno en el que un gen con alelos alternativos fijados de acuerdo a un patrón rígido explica una parte significativa de la variación; 2) Un proceso sucesivo de aplicar este modelo a todas las posiciones de interés, cada cM por ejemplo, a lo largo de todo el genoma o en una parte, verbigracia, un cromosoma; 3) Caracterización de un umbral de significación a nivel genómico que tenga en cuenta el hecho de que los diferentes estadísticos obtenidos en cada posición están correlacionados.

 

CRITICA

El barido genómico presenta una serie de problemas y limitaciones importantes. Algunos de ellos son: Etapa 1, el modelo que incorpora el QTL suele ser de gran ingenuidad y simpleza, por ejemplo, en un cruce F2 normalmente se asume que hay un solo QTL bialélico con cada alelo fijado en cada una de las líneas parentales; Etapa 2, este proceso resulta en una verosimilitud perfilada (y no en una verosimilitud sensu stricto) y, lo que es más preocupante, no tiene en cuenta el efecto del resto del genoma al calcular el estadístico en cada posición; Etapa 3) No es evidente que establecer un nivel de signicación a nivel genómico sea la estrategia más razonable, ya que la hipótesis nula que se pretende rebatir con este nivel de significacción es "No hay un QTL con efecto significativo en ninguna parte del genoma". Si la heredabilidad es distinta de cero, es evidente que debe haber una base genética para el carácter, y podemos obviar la labor del genotipado (R. L. Fernando, comunicación personal). Estos problemas no han pasado desapercibidos a los usuarios de la técnica y se han intentado resolver con diversas estrategias como el empleo de cofactores o la determinación de umbrales de significación mediante permutación, pero sin salir del paradigma clásico.

 

PROPUESTA

Proponemos un método que tiene en cuenta la variación en todo el genoma conjuntamente y que permite ser más flexible en cuanto al modelo a asumir a costa, en principio, de ser menos preciso en la localización de los posibles QTLs. Considérese que los datos de una población resultante de un cruce F2 entre las razas A y B se pueden modelar como

y = X b + Z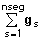 + e,

donde X y Z son matrices de incidencia, b, los efectos fijos, y el efecto del genoma se agrupa en nseg segmentos con efecto gs. Para cada segmento s se asume una distribución N[m_s, Var(s)]. El objetivo es dividir el genoma en segmentos de forma óptima, explicando el máximo de variación con el mínimo de parámetros. Se puede demostrar que

E ( y_i ) = X_i b + 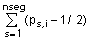D_s,

donde p_s,i es la proporción esperada del segmento con origen la raza A en el individuo i, D_s es la diferencia genotípica entre ambas razas atribuible a cada segmento. La varianza genética del individuo i es, aproximadamente,

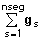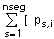
Var ( g_i ) = Var ( ) = + (1- p_s,i ) ]

y la covarianza entre los individuos i y j,

Cov ( g_i, g_j ) = + ] ,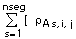

donde es la varianza genética atribuible al segmento s en la raza A, y es el coeficiente de correlación aditivo entre los individuos i y j atribuible a genes con origen de la raza A. De forma similar para la raza B. Los coeficientes p y r se pueden calcular mediante un algoritmo de Monte Carlo utilizando la información molecular disponible. Posteriormente, se pueden estimar b, D_s, , y mediante REML utilizando un algoritmo libre de derivadas.

 

RESULTADOS

Por falta de espacio, presentamos sólo uno de los casos analizados. Se simuló una población F2 de 400 individuos agrupados en 20 familias de hermanos y 2 de medios hermanos. El genoma consistió en un solo cromosoma de 60 cM, con 4 marcadores completamente informativos cada 20 cM. El carácter se determina por 40 genes de igual efecto promedio, 20 en el primer intervalo (0-20 cM) y 20 en el tercer intervalo (40 - 60 cM). Los efectos alélicos de cada gen se distribuyeron con media 0.0125 y -0.0125 en las razas A y B, respectivamente, y varianza 0.0125. La acción génica fue aditiva, tanto dentro como entre razas. Se generó una sola población base parental con una serie de alelos, utilizándose la misma población base en 20 réplicas. La varianza residual fue 1. Las varianzas genéticas (diferencias en medias entre líneas) atribuibles cada intervalo fueron: 0.387 (0.460), 0.0 (0.0), y 0.781 (0.414). La media esperada en la F2 fue 0.404.

Se dividió el cromosoma en tres intervalos, delimitados por los marcadores. Se compararon tres estrategias de análisis. En el mapeo de segmentos (MS) se incluyeron en el modelo dos segmentos, uno con el intervalo i (i=1, 3) más otro con los otros dos intervalos. Se estimaron las medias y varianzas genéticas correspondientes a cada segmento en las tres combinaciones. En la opción regresión (R) se estimaron las diferencias entre medias de genotipos para cada intervalo de forma independiente (esta estrategia es la equivalente a la utilizada habitualmente cuando se asumen alelos fijados en cada línea). En la opción anova (V) se estimaron las varianzas genéticas atribuibles a cada intervalo de forma independiente (esta estrategia es similar al método ML o REML para estimar la varianza debida a un QTL). En todos los análisis se asumió que la varianza aditiva era la misma en ambas razas dentro de cada segmento, = . Los resultados están en la Tabla.

 

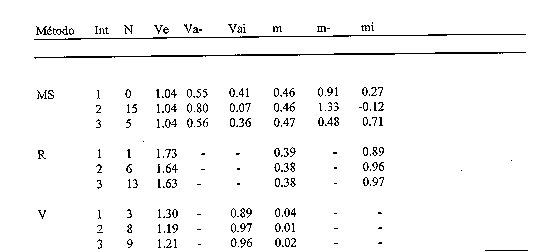
Int es el intervalo considerado de forma aislada, N es el número de veces que una combinación dio la máxima verosimilitud, Ve es la varianza residual, Vai es la varianza aditiva del segmento que incluye un solo intervalo, Va- es la varianza aditiva del resto del cromosoma, m es la media general, mi es la diferencia media entre razas atribuible al segmento que incluye un solo intervalo, m-, la atribuible al resto del genoma

La situación genética presentada es, quizá, una de las que presenta mayor complicación, no sólo hay dos ‘clusters’ de genes disjuntos, sino que los alelos no están fijados en ninguna de las líneas y en promedio el efecto de los genes también difiere entre líneas. A pesar de ello, MS permite extraer una serie de consecuencias interesantes. Nótese que el modelo de dos segmentos más plausible en MS es aquél que divide los segmentos entre los que contribuyen o no a la expresión del carácter (intervalo 2 versus 1+3), en segundo lugar el que incluye el intervalo con más efecto (intervalo 3) versus los demás. Además, MS identifica correctamente que no hay variación en el intervalo intermedio, lo que no ocurre en las otras estrategias. En 12 réplicas la estima de Ve(2) fue < 0.01. El método R resulta en estimas muy sesgadas de Ve, mientras que V resulta en estimas muy sesgadas de mi. Asimismo, R detecta sólo uno de los intervalos con QTLs (el 3), mientras que V no identifica ningún intervalo de forma clara. Las estimas V y R de cada intervalo incluyen la variación del resto del genoma.

 

LIMITACIONES

Un problema importante es cómo realizar tests de significación (lo más razonable es un test de cociente de verosimilitudes, pero sólo se puede aplicar a modelos jerarquizados) y la estrategia a seguir para definir el modelo más plausible. Nótese que en SM es inmediato tener en cuenta la dominancia si se asumen alelos fijados en cada línea, al igual que con regresión.

 

RECOMENDACIONES

A falta de investigar más en detalle el comportamiento de este método, lo más razonable parece comparar las estrategias disponibles clásicas con este método. Si no hay grandes discrepancias, el modelo más sencillo asumido en las estrategias R o V será el más plausible. Como primer análisis, se recomienda estimar la heredabilidad y las diferencias entre medias atribuibles a cada cromosoma de forma independiente.

 

Agradecimientos : Trabajo financiado gracias a los proyectos AGF96-2510 (CICYT) y BIO-CT97-962243 (UE).